B Tree
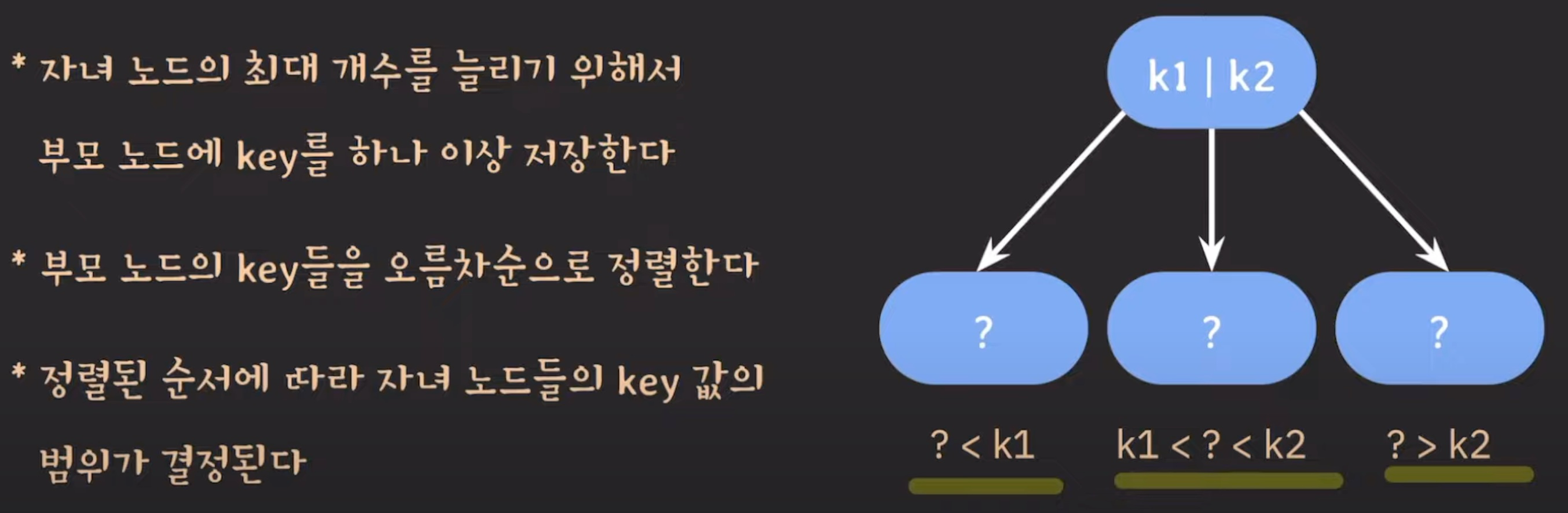
Tree 자료구조에서 여러 개의 자식을 가질 수 있는 트리를 말한다.
⚠️
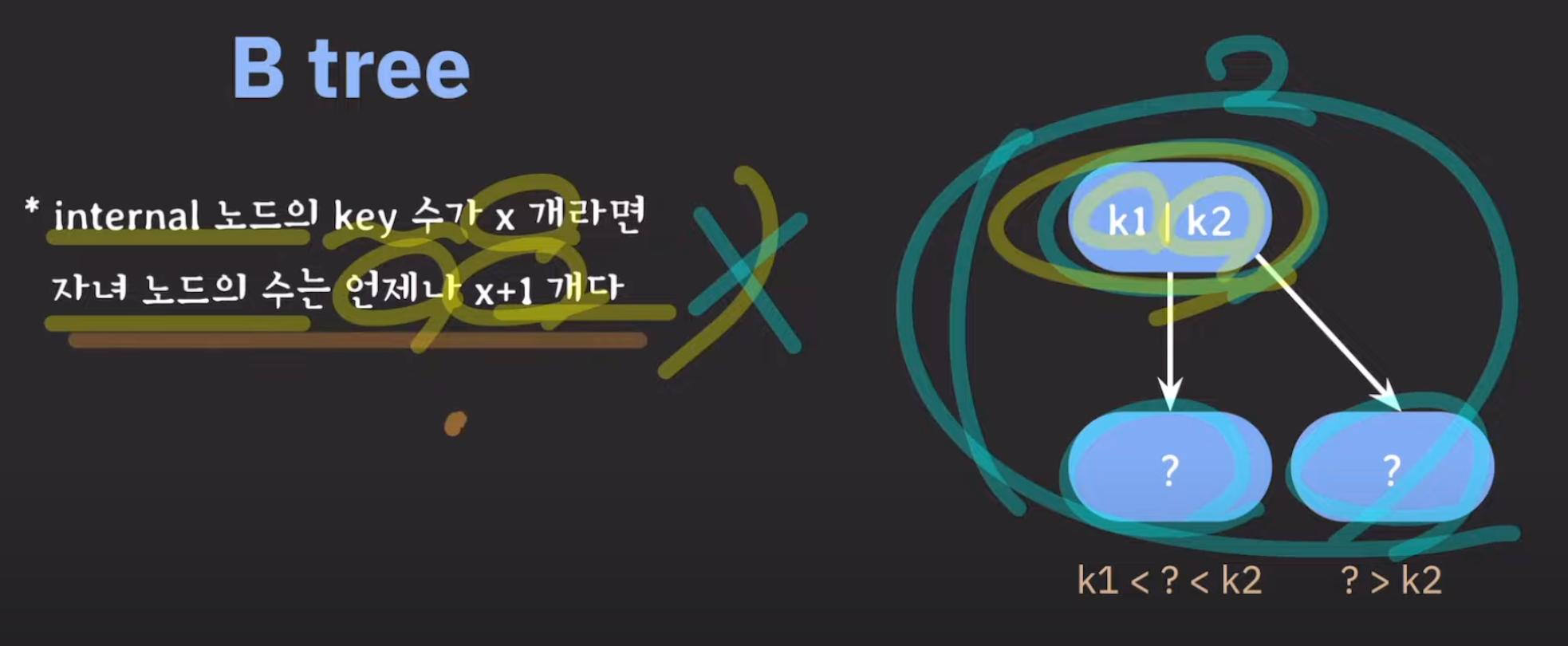
internal node의 key수가 X개라면 자녀 노드의 수는 반드시 X+1개여야 한다.
👇는 잘못된 예시
B Tree의 차수

M차 B Tree란 내부 노드의 자식 수가 최대 M가 될 수 있는 B Tree를 말한다.
예를 들어, 3차 B Tree의 경우
- 최소 자녀 수 : (3/2) = 1.5 👉 0.5는 반올림 👉 2
- 최소 key 수 : 최소 자녀 수 - 1 = 1
B Tree 삽입
- 추가는 항상 leaf 노드에 한다.
- 노드가 넘치면 가운데 key를 기준으로 좌우 key들은 분할하고 가운데 key를 승진한다.
B Tree 삭제
- 삭제도 항상 leaf 노드에서 한다.
- 삭제 후 최소 key 수보다 적어졌다면 재조정 한다.
- 최소 key 수 : (M/2) - 1
형제 노드가 최소 key 수를 가지고 있는 경우
- 형제 노드에서 key를 빌려와서 삭제된 노드에 삽입한다.

형제 노드가 최소 key 수를 만족하지 못하는 경우
- 형제 노드와 병합한다.

부모가 지원해준 뒤 부모한테 문제가 생긴 경우

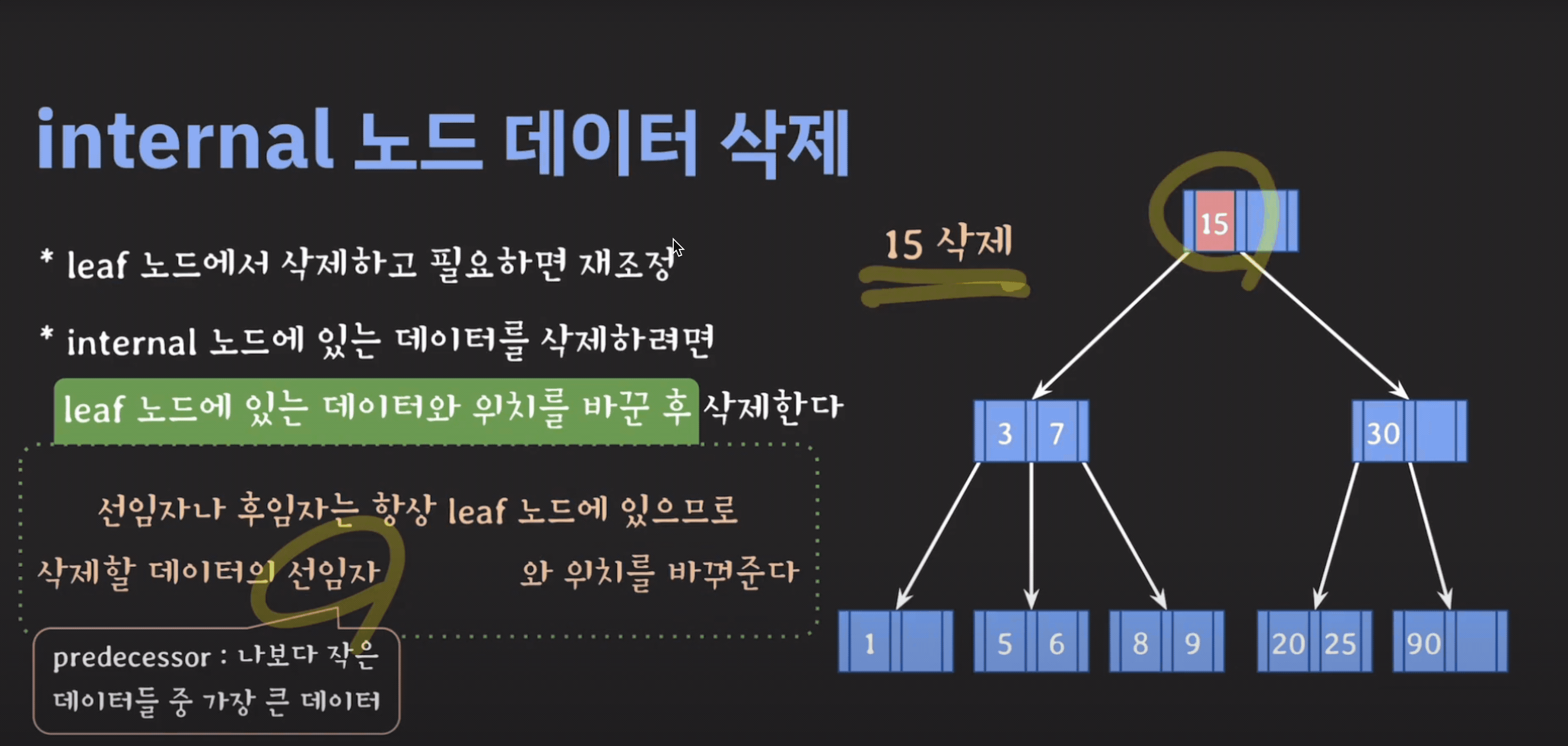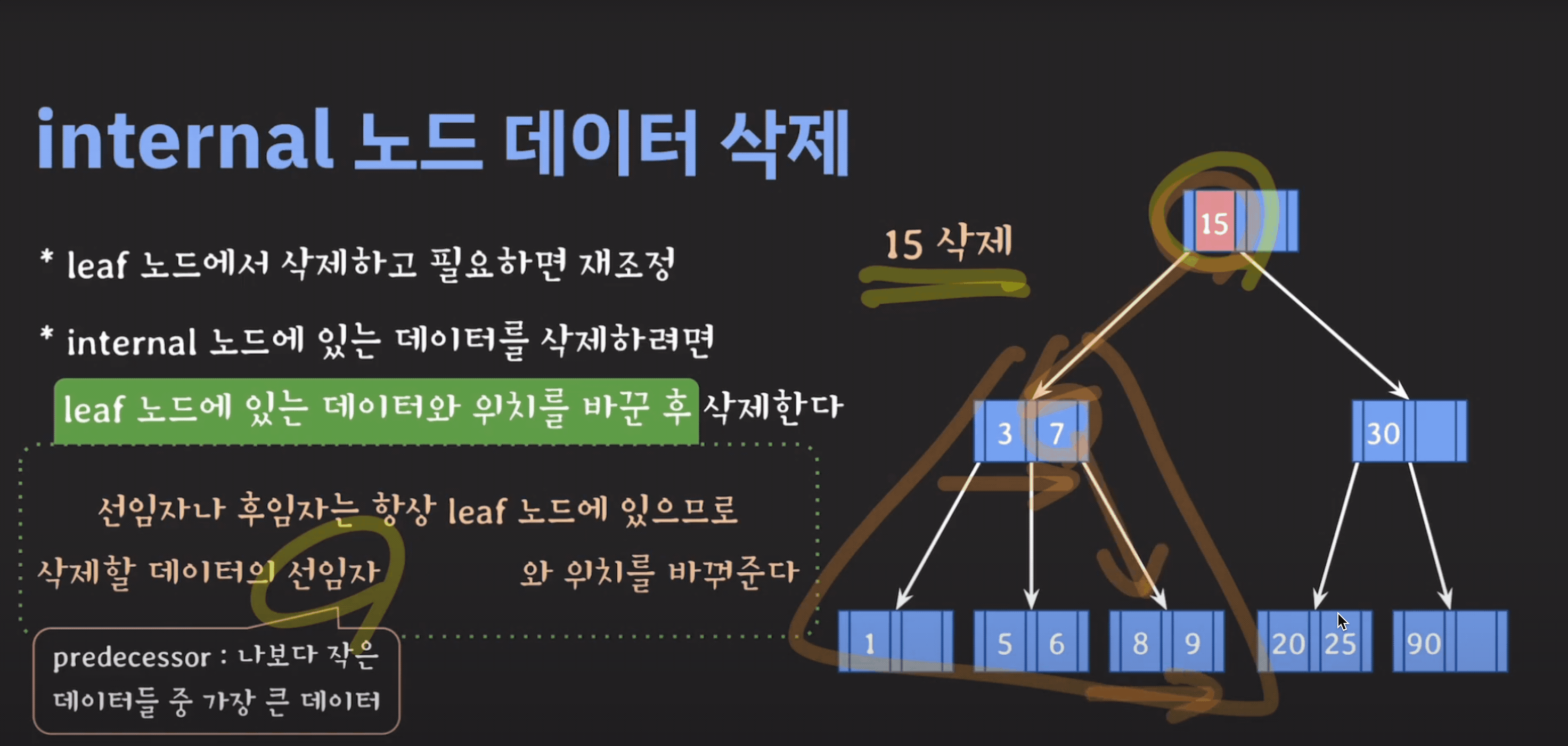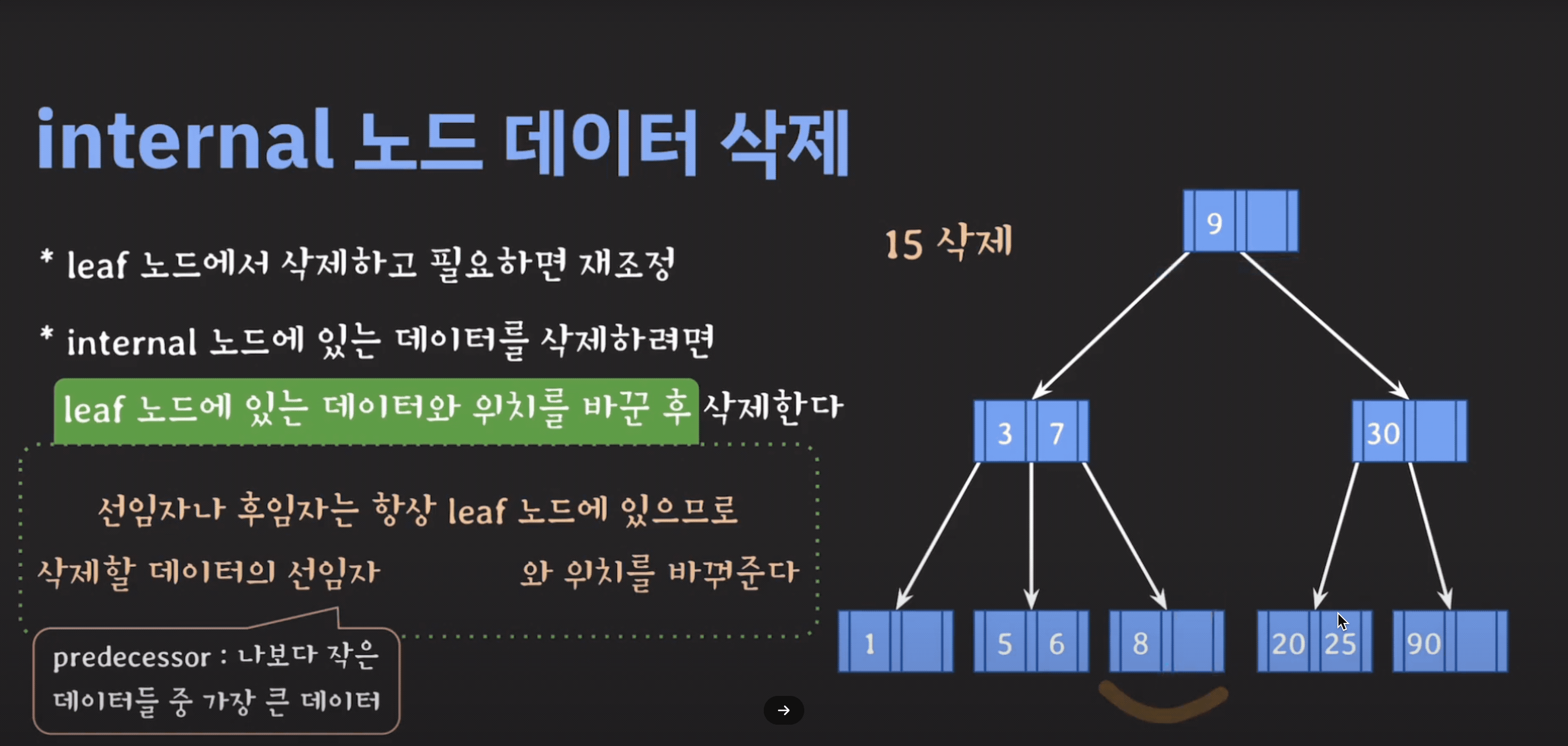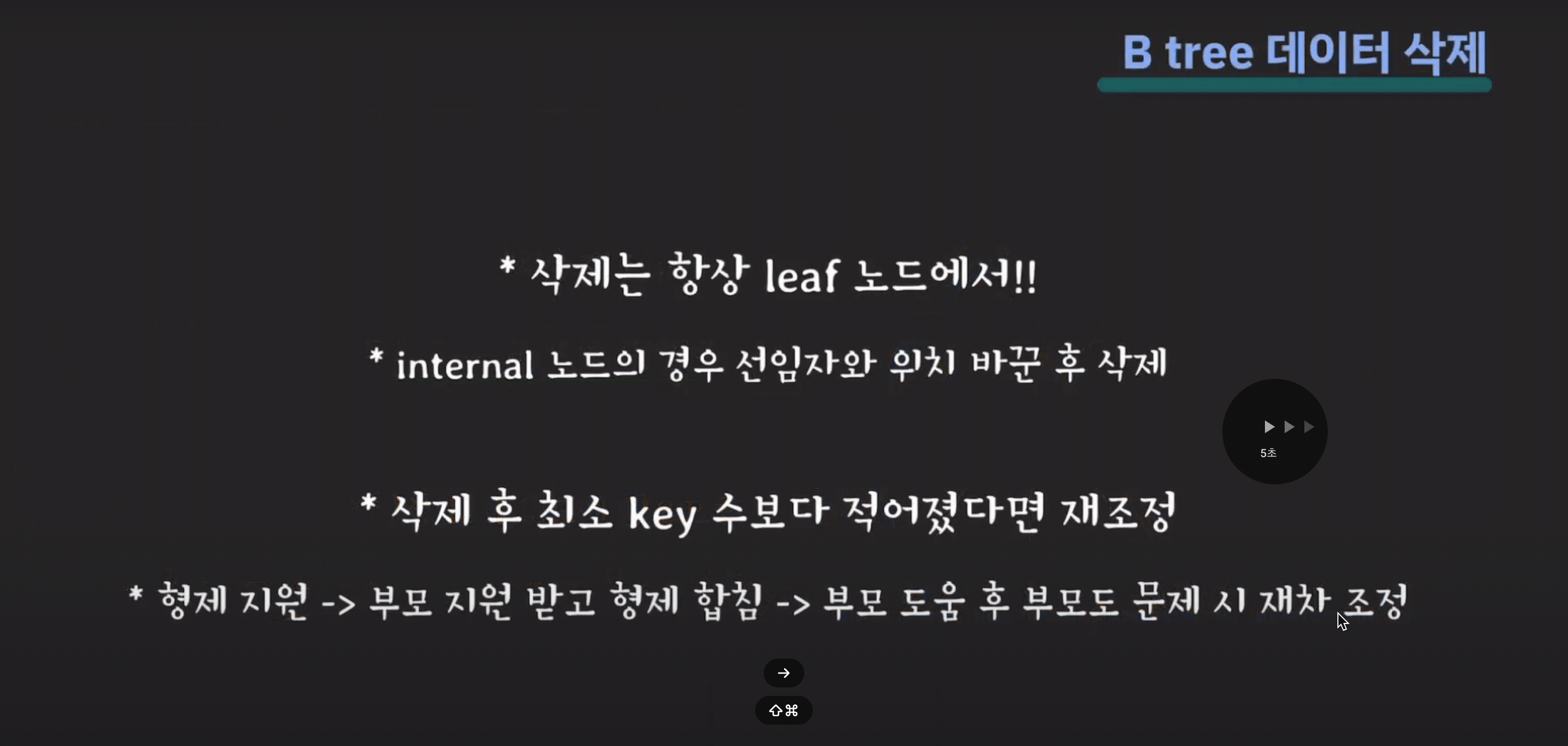
internal node 삭제
- 삭제할 데이터의 선임자나 후임자와 위치를 바꾼다.
- 선임자(predecessor) : 왼쪽 서브트리에서 가장 큰 값
- 후임자(successor) : 오른쪽 서브트리에서 가장 작은 값
- 삭제할 데이터를 삭제한다.
시간 복잡도
- 탐색, 삽입, 삭제 모두 O(logN)이다.
- 바이너리 서치 트리는 오른쪽에만 자식 노드가 쌓이는 형식으로 트리가 성장한다면 O(N)이 될 수 있다.
-

- 이런 현상을 막기 위해서 self-balancing tree가 나왔다.
- AVL Tree, Red-Black Tree
-
B Tree를 사용하는 이유
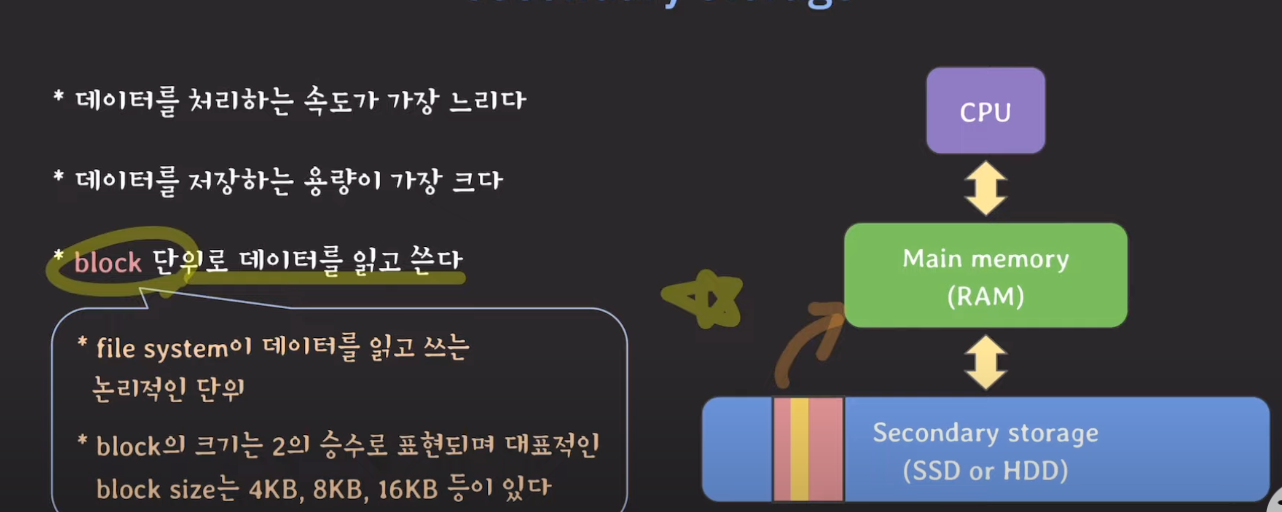
Secondary Storage 특징

- 데이터를 처리하는 속도가 가장 느리다.
- 데이터를 저장하는 용량이 가장 크다.
- block 단위로 데이터를 읽고 쓴다.
-
- 불필요한 데이터까지 읽어올 가능성이 있다.
-
DB의 관점
- Secondary Storage에 저장이 된다.
- DB에서 데이터를 조회할 때 Secondary Storage에 최대한 적게 접근하는 것이 성능면에서 좋다.
- block 단위로 데이터를 읽고 쓰기 때문에 연관된 데이터를 모아서 저장하면 더 효율적으로 읽고 쓸 수 있다.
B+Tree
- B-tree를 개선해서 등장
- 모든 리프 노드들은 링크드 리스트 형태로 이어져 있음
- full scan 시, 리프 노드들만 순차 탐색하면 되기 때문에 탐색에 유리함
- B-tree는 탐색 시, 모든 노드를 탐색해야 함
- 실제 데이터는 리프 노드에만 저장됨
- 내부 노드들은 단지 키만 가지고 있고, 올바른 리프 노드로 연결해주는 라우팅 기능을 함
- B-tree에 비해 같은 노드에 더 많은 키를 저장할 수 있음
- 중복 키를 가짐
- 내부 노드들이 데이터를 가지고 있지 않기 때문에 리프 노드들이 키와 데이터를 모두 가지고 있어야 함
B+Tree 장점
- 리프 노드를 제외하고 데이터를 담아두지 않기 때문에 메인 메모리를 더 확보해 더 많은 key를 수용할 수 있음
- 하나의 노드에 더 많은 key들을 담을 수 있기 때문에 트리의 높이는 더 낮아짐
- cache hit를 높일 수 있음
- 풀 스캔 시, B+tree는 리프 노드에 데이터가 모두 있어 한 번의 선형 탐색만 하면 됨
- B-tree에 비해 빠름
B-tree와 B+tree의 비교
| 비교 | B-tree | B+tree |
|---|---|---|
| 데이터 저장 | 모든 내부, 리프 노드들이 데이터를 가짐 | 리프노드만 데이터를 가짐 |
| 검색 속도 | 모든 노드 검색, 느림 | 리프노드에서 선형 탐색 |
| 키 중복 | 없음 | 있음 |
| 삭제 | 내부 노드의 삭제는 보잡하고 트리 변경히 많음 | 어떠한 노드든 리프에 있기 때문에 삭제가 쉬움 |
| 링크드 리스트 | 존재 x | 리프 노드는 링크드 리스트로 저장됨 |
| 높이 | 특정 갯수의 노드는 높이가 높음 | 같은 노드일 때 B-tree보다 높이가 낮음 |
| 사용 | 데이터베이스, 검색엔진 | 멀티레벨 인덱스, DB 인덱스 |