Hash

해시 자료구조는 키-값 쌍을 저장하는 자료구조입니다. 해시 함수를 사용하여 키를 해시 값으로 변환하고, 이를 통해 데이터를 저장 및 검색합니다. 해시 함수는 키를 고정 길이의 값으로 변환하는 함수입니다. 해시 자료구조는 빠른 검색 속도를 제공하지만, 해시 충돌이 발생할 수 있습니다. 해시 충돌은 서로 다른 키가 동일한 해시 값을 가질 경우 발생합니다.

Direct Addressing

Direct Addressing은 해시 함수를 사용하지 않고, 키 값을 직접 주소로 사용하여 데이터를 저장하고 탐색하는 방식입니다.

실제 저장되는 키의 개수가 가능한 키의 모든 개수에 비해 상대적으로 적을 때 해시 테이블을 사용한다.

해시함수

임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수이다. 예를 들어서 아스키 코드표를 보면 A 라는 값에 대한 key를 탐색하는 비용은 O(1), 상수시간이 걸리게 된다. 왜냐면 A라는 값이 65번지에 있는 것을 알고 있기 때문이다.

이처럼 해시함수를 사용해서 나오는 고정된 길이의 데이터 를 주소로 사용해서 탐색 시간을 O(1)으로 줄일 수 있다.

충돌

해시함수가 아무리 잘 구현되었다고 하더라도 해시 함수의 결과가 같을 수 있다. 즉, 다른 두 키에 대해서 같은 주소에 데이터가 저장되게 되는 것이다. 이를 해결하기 위한 방법으로는 크게 체이닝(Chaining)과 개방 주소법(Open Addressing) 이 있다.

체이닝 (Chaining)

해시 테이블의 슬롯을 연결 리스트로 구현하는 방법이다. 이 방법은 연결 리스트로 인해 최악의 경우 수행시간이 O(n)이 된다는 단점이 있다.

void AddHashData(int key, Node *node)
{
    int hash_key = HASH_KEY(key);
    if  (hashTable[hash_key] == NULL)    
    {
        hashTable[hash_key] = node;
    }
    else     
    {
        node->hashNext = hashTable[hash_key];
        hashTable[hash_key] = node;
    }
}

개방 주소법(Open Addressing)

개방 주소법에는 선형 탐사(Linear Probling), 이차 탐사(quadratic Probling), 이중 해싱(Double Hashing) 등의 충돌 해결 방식이 있습니다.

선형 탐색(Linear Probling)

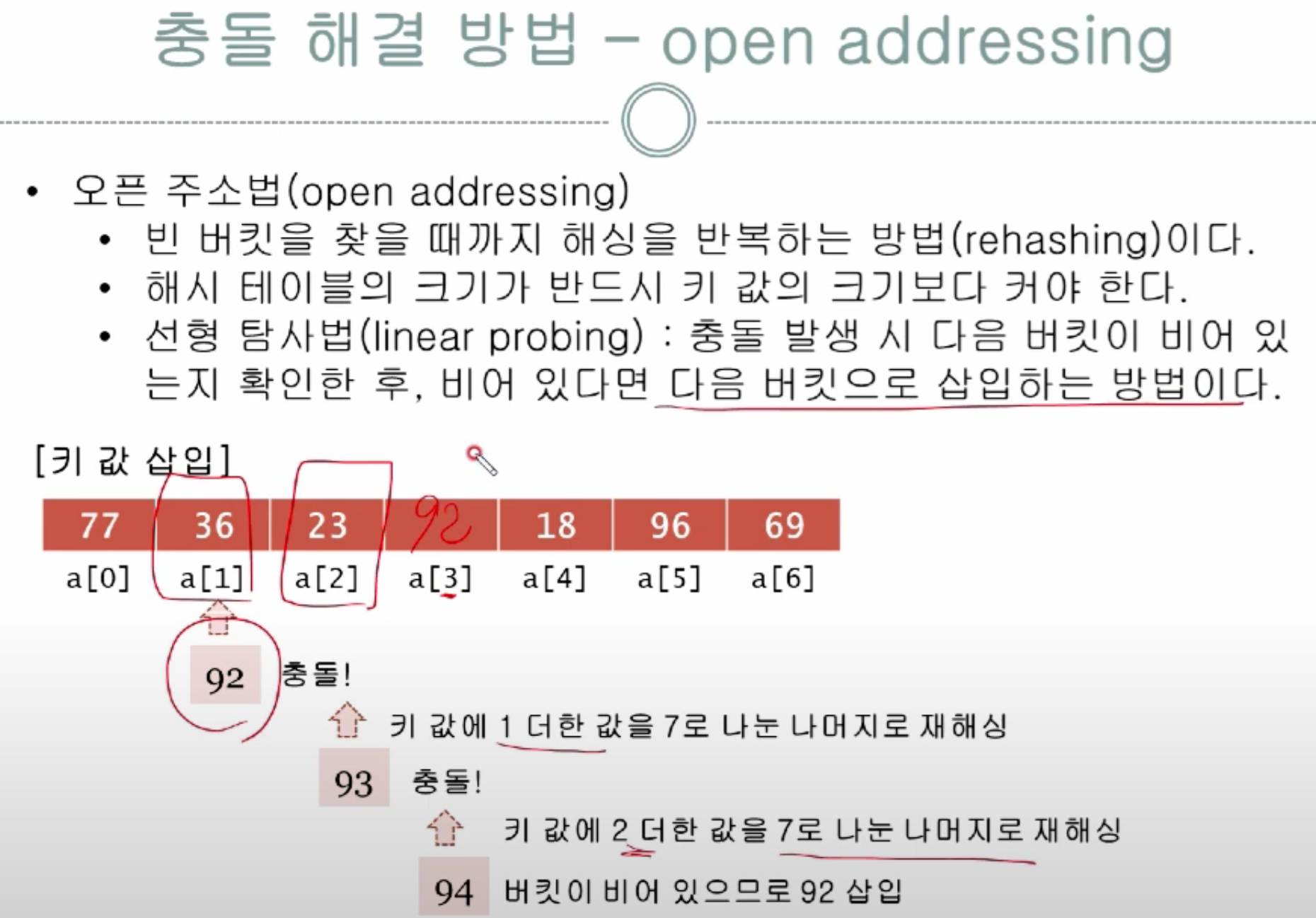
선형 프로빙은 구현이 매우 쉬우나 primary clustering이라는 단점이 존재한다. primary clustering은 한 번 충돌이 나면 집중적으로 충돌이 발생하는 것을 의미한다. 이로 인해 평균 검색 시간이 증가한다.

추가방법

void hash_lp_add(element item, element ht[]) {
    int i, hash_value;
    hash_value = i = hash_function(item.key);
    
    while(!empty(ht[i])) {
        if(equal(item, ht[i])) {
            fprintf(stderr, "탐색키가 중복되었습니다.\n");
            exit(1);
        }
        i = (i + 1) % TABLE_SIZE;
        if(i == hash_value) {
            fprintf(stderr, "테이블이 가득찼습니다.");
            exit(1);
        }
    }
    ht[i] = item;
}

탐색방법

void hash_lp_search(element item, element ht[]) {
    int i, hash_value;
    hash_value = i = hash_function(item.key);
    while(!empty(ht[i])) {
        if(equal(item, ht[i])) {
            fprintf(stderr, "탐색 %s: 위치 = %d\n", item.key, i);
            return;
        }
        i = (i + 1) % TABLE_SIZE;
        if(i == hash_value) {
            fprintf(stderr, "찾는 값이 테이블에 없음");
            return;
        }
    }
    fprintf(stderr, "찾는 값이 테이블에 없음\n");
}

이차 탐사법(Quadratic Probing)

선형 조사법은 1씩 증가했던 것과는 달리 이차 조사법은 제곱수씩 더해서 조사할 위치를 정하는 방식이다.

이차식 탐사법은 선형 탐사법에 비해 충돌이 적지만 secondary clustering이 발생한다. secondary clustering은 처음 충돌한 위치가 같다면 다음 충돌할 위치도 반복적으로 충돌이 나게 된다는 의미이다.

추가방법

void hash_qp_add(element item, element ht[]) {
    int i, hash_value, inc = 0;
    hash_value = i = hash_function(item.key);
    while(!empty(ht[i])) {
        if(equal(item, ht[i])) {
            fprintf(stderr, "탐색키가 중복되었습니다\n");
            exit(1);
        }
        i = (hash_value + inc * inc) % TABLE_SIZE;
        inc = inc + 1;
        if(i == hash_value) {
            fprintf(stderr, "테이블이 가득 찼습니다.\n");
            exit(1);
        }
    }
    ht[i] = item;
}

이중 해싱 (Double Hashing)

항목을 저장할 다음 위치를 결정할 때, 원래 해시 함수와 다른 별개의 해시 함수를 같이 이용하는 방법이다.

두 개의 해시 함수를 써야하고 구현이 복잡할 수 있다는 단점이 존재하지만 충돌이 일어날 확률이 가장 적다.

추가방법

void hash_dh_add(element item, element ht[]) {
    int i, hash_value, inc;
    hash_value = i = hash_function(item.key);
    inc = hash_function2(item.key);
    // printf("hash_address=%d\n", i);
    while(!empty(ht[i])) {
        if(equal(item, ht[i])) {
            fprintf(stderr, "탐색키가 중복되었습니다.\n");
            exit(1);
        }
        i = (i + inc) % TABLE_SIZE;
        if(i == hash_value) {
            fprintf(stderr, "테이블이 가득 찼습니다.\n");
            exit(1);
        }
    }
    ht[i] = item;
}

Load Factor (부하율)

전체 키 개수 / 해시 테이블의 크기

부하율은 해시 함수가 키를 균일하게 분배하는지 알 수 있다.
부하율이 1보다 작으면 리스트의 노드가 비어 있는 경우로 메모리가 낭비될 수 있다.
부하율이 1보다 크면 리스트의 노드가 두 개 이상인 경우로 검색, 삭제의 시간이 다소 느려질 수 있다.

Reference

https://moneylogging.tistory.com/entry/자바-개방주소법 (opens in a new tab)

https://ryu-e.tistory.com/87 (opens in a new tab)

https://huiyu.tistory.com/entry/자료구조-체이닝-해시-테이블Chaining-Hash-Table (opens in a new tab)

https://www.youtube.com/results?search_query=오픈+주소법 (opens in a new tab)

https://laurent.tistory.com/entry/자료구조-개방-주소법-Open-Addressing-선형-조사법-이차-조사법-이중-해시법 (opens in a new tab)

서블릿 B Tree