LCS (Longest Common Subsequence)
LCS는 최장 공통 부분 수열이라는 뜻으로써, 부분 수열 중에서 공집합이 되는 수열 중 최장 길이를 계산하는 문제다.
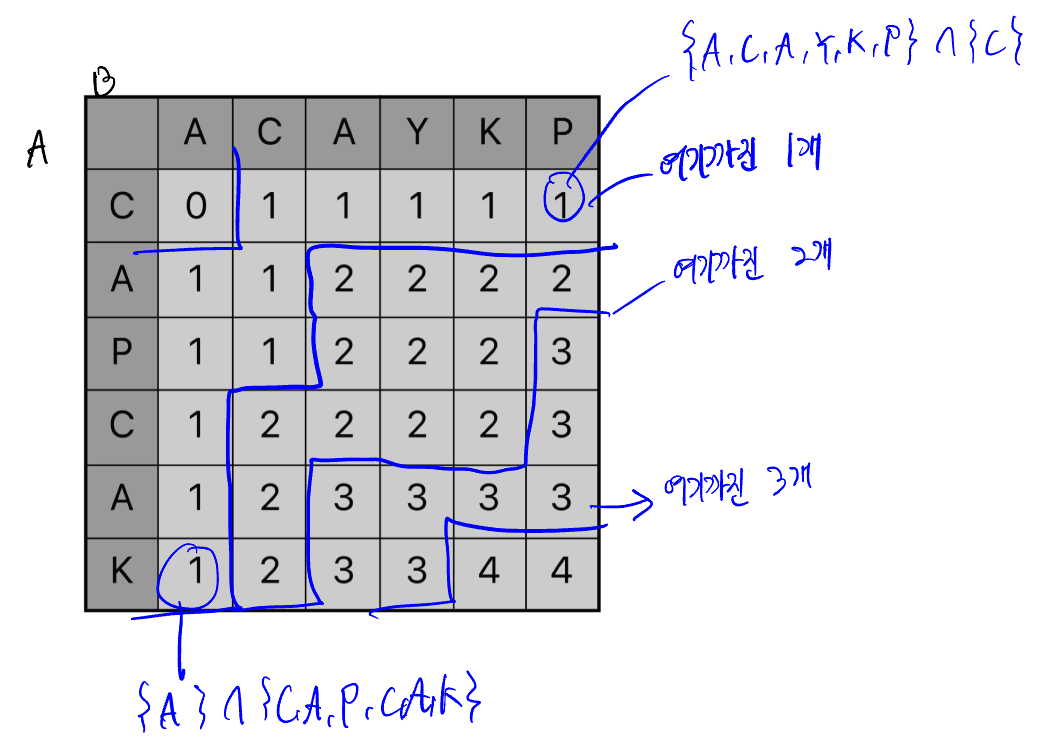
ACAYKP
CAPCAK이렇게 두 문자열이 있을 때 이 문자열로 만들 수 있는 조합 중에서 교집합이 되는 가장 긴 문자열을 찾으면 되는데, DP의 일종으로 풀 수 있다.
예를 들어서
{A} 와 {CAPCAK}의 최장 길이 교집합은 {A}로, 1이다.
{AC}와 {CAPCAK}의 최장 길이 교집합은 {AC}로, 2이다.
이런식으로 첫 번째 문자열의 마지막 인덱스를 i, 두 번째 문자열의 마지막 인덱스를 j라고 하자.
0 ~ i, 0 ~ j까지를 탐색하면서 DP를 갱신하는데, i보다 크거나 j보다 크면 dp[i][j]보다 무조건 크거나 같다. 그리고 현재의 i와 j가 동일하면 i - 1, j - 1의 값에 1을 더해주면 된다.
풀이
import java.io.*;
import java.util.*;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer st;
static Set<String> swapped = new HashSet<>();
static int ans = Integer.MAX_VALUE;
public static void main(String[] args) throws Exception {
st= new StringTokenizer(br.readLine());
char[] str1 = st.nextToken().toCharArray();
st= new StringTokenizer(br.readLine());
char[] str2 = st.nextToken().toCharArray();
int length1 = str1.length;
int length2 = str2.length;
int[][] dp = new int[length1 + 1][length2 + 1];
for(int i = 1; i <= length1; i++) {
for(int j = 1; j <= length2; j++) {
// (i-1)과 (j-1) 번째 문자가 서로 같다면
if(str1[i - 1] == str2[j - 1]) {
// 대각선 위 (i-1, j-1)의 dp에 +1 한 값으로 갱신
dp[i][j] = dp[i - 1][j - 1] + 1;
}
// 같지 않다면 이전 열(i-1)과 이전 행(j-1)의 값 중 큰 것으로 갱신
else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// Top-Down 때와는 다르게 dp 인덱스가 한 줄씩 추가되었으므로 -1을 하지 않음
System.out.println(dp[length1][length2]);
}
}