Algorithm
Dynamic Programming

Dynamic Programming(DP)

문제에 대한 정답이 될 가능성이 있는 모든 해결책을 "체계적"이고 "효율적"으로 탐색하는 풀이법

  1. 크고 복잡한 문제를 작은 문제들로 나눈다.
  2. 하위 문제의 답을 계산한다.
  • 중복 계산해야 하는 하위 문제가 있다. (overlapping subproblems - 중복 하위 문제)
  • 한 번 계산한 결과는 메모리에 저장하여 재계산하지 않도록 한다. => 속도향상 (memoization, dp table)
    • Top Down 방식에 저장하는 메모리 : memoization
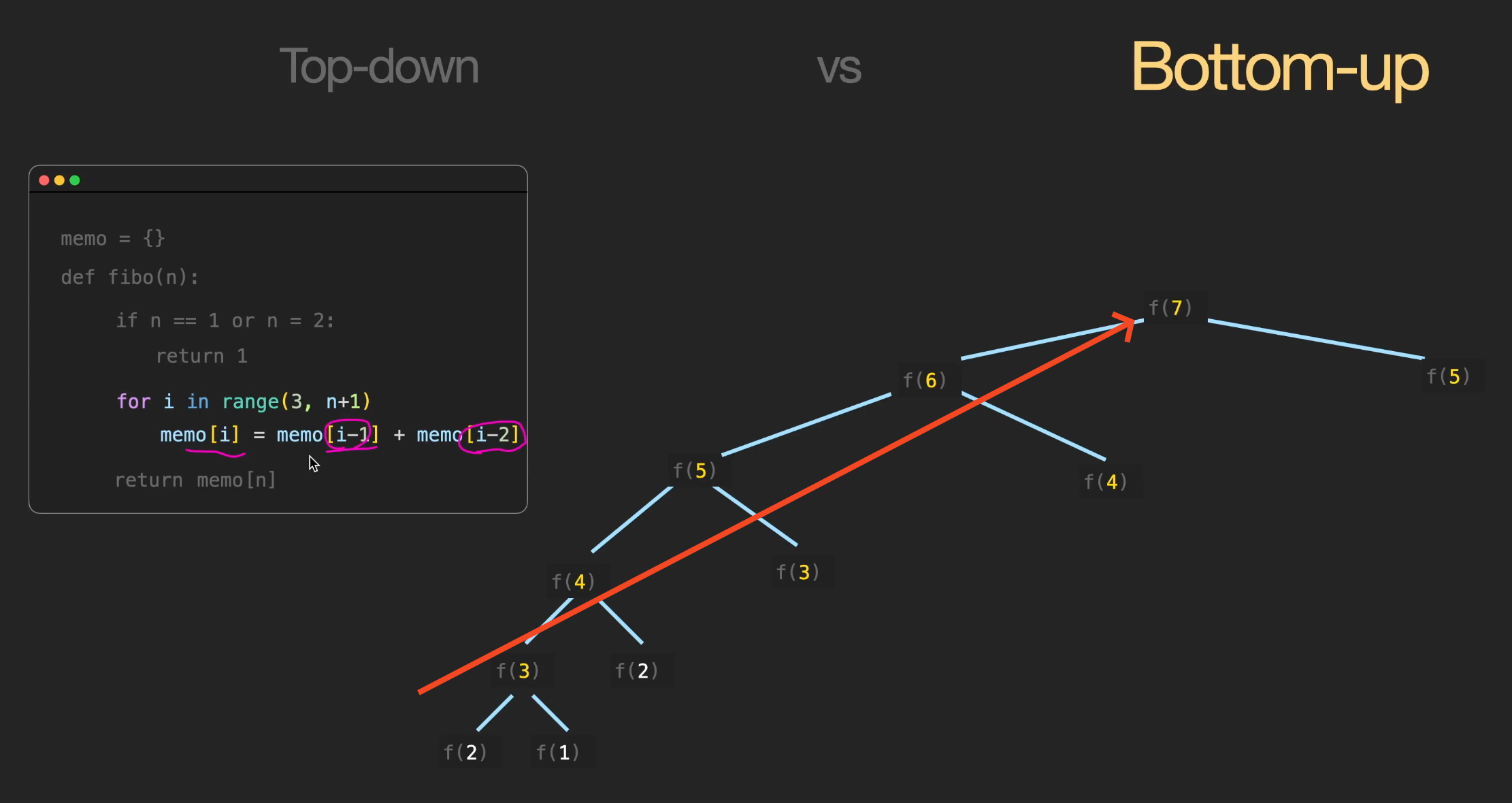
    • Bottom Up 방식에 저장하는 메모리 : dp table
  1. 하위 문제에 대한 답을 통해 원래 문제에 대한 답을 계산한다. (optimal substructure - 최적 부분 구조)
  • 최적 부분 구조 : 하위 부분 문제에서 구한 최적의 답이 합쳐진 큰 문제의 최적의 답을 구할 수 있는 구조

Top Down vs Bottom Up

  • Top Down : 큰 문제를 작은 문제로 나누어 해결하는 방법
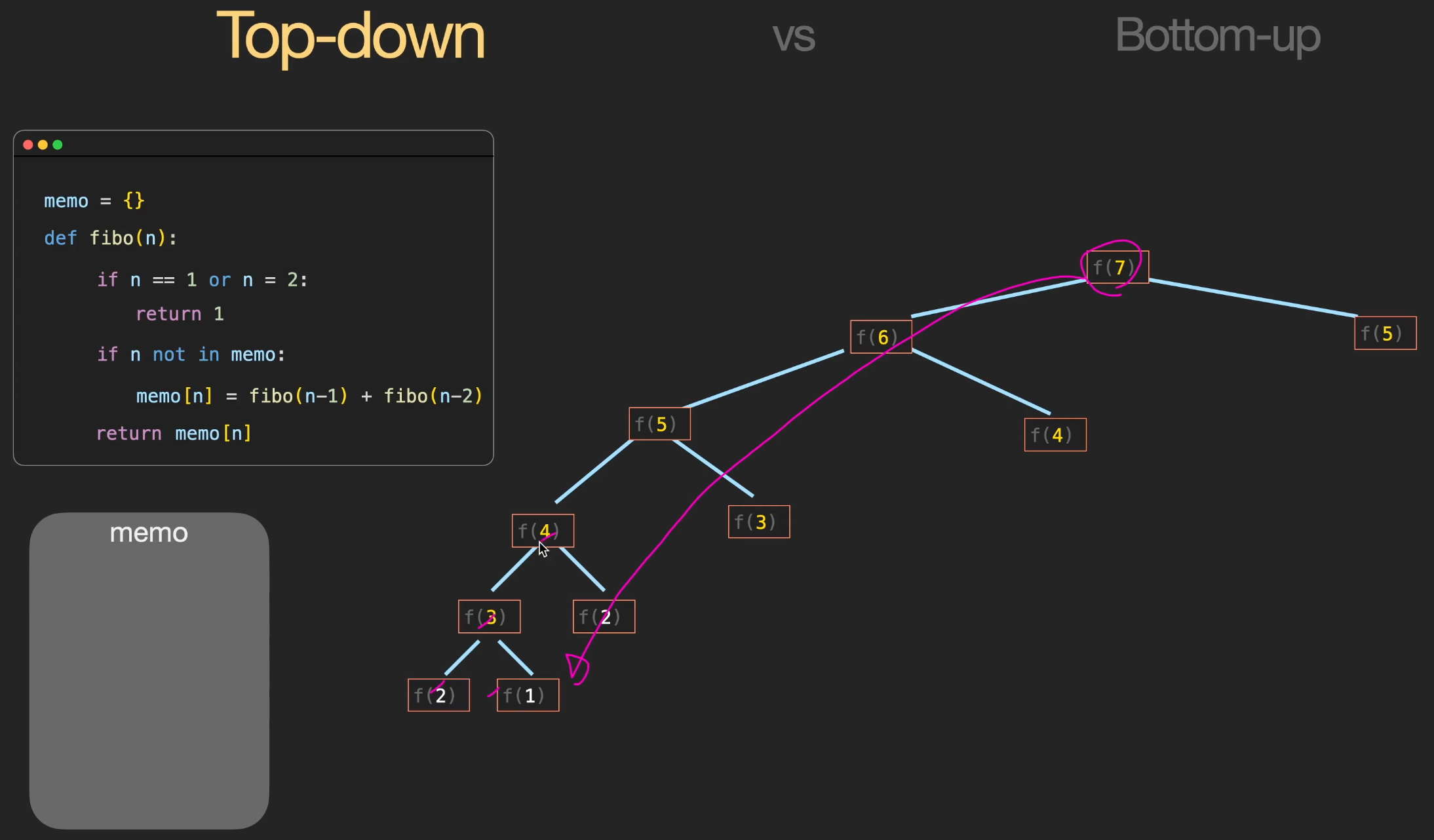
  • Bottom Up : 작은 문제부터 차근차근 답을 도출하는 방법

삽질일기

대충 강의 듣다가 fibonacci 수열을 dp로 어떻게 구현해야할지 떠올라서 구현을 해보았다.

memory = {}
def fibo_dp(n) :
  if n == 1 or n == 2 : 
    return 1
  
  if n-1 in memory : 
    memory[n] = memory[n-1] + fibo_dp(n-2)
    return memory[n]
  elif n-2 in memory :
    memory[n] = memory[n-2] + fibo_dp(n-1)
    return memory[n]
  elif n-2 in memory and n-1 in memory : 
    memory[n] = memory[n-1] + memory[n-2]
    return memory[n]
  
  memory[n] = fibo_dp(n-1) + fibo_dp(n-2)
  return memory[n]

짜잔🌟

구현하고보니 코드가 더러웠다. 그래서 조금 중복되는 부분을 정리해줬다.

memory = {}
def fibo_dp(n) :
  if n == 1 or n == 2 : 
    return 1
  
  if n-2 in memory and n-1 in memory : 
    memory[n] = memory[n-1] + memory[n-2]
  elif n-2 in memory :
    memory[n] = memory[n-2] + fibo_dp(n-1)
  elif n-1 in memory : 
    memory[n] = memory[n-1] + fibo_dp(n-2)
  else : 
    memory[n] = fibo_dp(n-1) + fibo_dp(n-2)
 
  return memory[n]

그리고 강사님의 솔루션은 다음과 같았다.

def fibo_dp(n) : 
  if n == 1 or n == 2 : 
    return 1
  
  if n not in memory : 
    memory[n] = fibo(n-1) + fibo(n-2)
  
  return memory[n]

근데 이 두 코드를 실행해보고나니 실행 속도가 강사님이 설명해주신 코드가 더 빨랐던 것이다.
디버깅도 해보고 몇몇 수정을 거쳤지만(처음에는 fibo_dp 함수가 아니라 fibo 함수를 호출하고 있었고 다음 함수를 호출하기 전에 memory를 초기화해주는 부분도 없었다.) 여전히 강사님이 구현한 함수가 더 실행속도가 빨랐다.
내 추측은 아니고 다른 분의 추측은 if ~ else 구문을 통과하면서 검색을 3번이나 하기 때문에 거기에서 발생하는 비용으로 인해서 속도가 느려진다는 것이었고 나도 그 부분에 어느정도 동의를 했다. Python의 Hash Search는 N(1)의 시간복잡도를 가지지만 그것도 역시 시간복잡도긴 하니까.

배운점

  1. 일단 검색에도 비용이 든다.라는 중요한 교훈을 얻었다. 문제를 풀 때 보통 정렬까지는 시간비용을 계산하면서 검색은 시간비용을 계산하지 않는다는 것을 깨달았다.
  2. 벤 다이어 그램을 잘 생각해봐야 할 것 같다는 생각이 들었다. 예를 들면 첫 번째 구현에서 해당하는 부분은
    "else에 해당하는 부분이 조건1이거나 조건2이거나 조건1과 조건2를 충족하지 못하는 것"인데, 이는 다른 말로 하면 "조건1도 조건2도 아닌 것"이 된다.
elif n-2 in memory :
  memory[n] = memory[n-2] + fibo_dp(n-1)
elif n-1 in memory : 
  memory[n] = memory[n-1] + fibo_dp(n-2)

내가 예외로 발생할 수 있다고 생각한 이 부분에서 디버그 포인트를 찍어보면 1번 밖에 실행이 되지 않는다. 그 1번은 n이 4일 경우, 즉 3은 들어있는데 2는 들어있지 않는 경우뿐이다. (1과 2는 메모리에 넣어주지 않으므로)
결론적으로 if n not in memory : 라는 조건문과 내가 사용한 4중 if ~ else문은 동일한 동작을 하게 된다.

  1. 조건문을 짤 때 첫 번째 조건에 유의하자.

사실 내가 처음에 짯던 코드의 조건문은

if n-1 in memory : 
elif n-2 in memory :
elif n-2 in memory and n-1 in memory : 
else :

이거였다. 즉,

elif n-2 in memory and n-1 in memory :

이 조건은 들어올 일이 없는 것이다. 조건문은 넓은 범위 -> 좁은 범위이 아니라🙅 좁은 범위 -> 넓은 범위가 되어야 한다.

그래프Dijkstra