List에서 Tree 연산
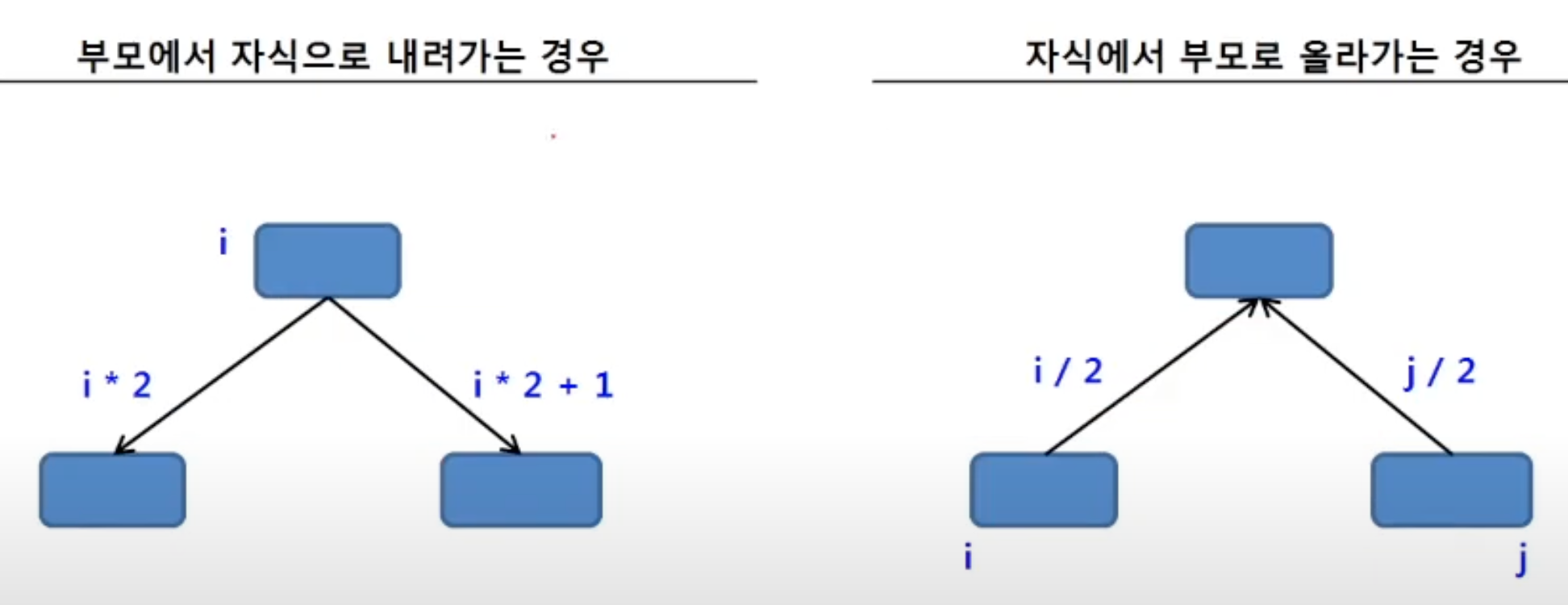
이진 트리
class Node :
def __init__(self, value = 0, left = None, right = None) :
self.value = value
self.left = left
self.right = right
class BinaryTree :
def __init__(self) :
self.root = None
bt = BinaryTree()
bt.root = Node(value=1)
bt.root.left = Node(value=2)
bt.root.right = Node(value=3)
bt.root.left.left = Node(value=4)
bt.root.left.right = Node(value=5)
bt.root.right.left = Node(value=6)
bt.root.right.right = Node(value=7)일반적인 트리
class Node:
def __init__(self, data):
self.data = data
self.children = []
def add_child(self, node):
self.children.append(node)
class Tree:
def __init__(self, root):
self.root = Node(root)
def print_tree(self):
self._print_tree(self.root)
def _print_tree(self, node, level=0):
print(' ' * level + str(node.data))
for child in node.children:
self._print_tree(child, level+1)
tree = Tree('root')
tree.root.add_child(Node('child_1'))
tree.root.add_child(Node('child_2'))
tree.root.children[0].add_child(Node('child_1_1'))
tree.root.children[0].add_child(Node('child_1_2'))
tree.print_tree()BFS (Breadth-First Search)
너비 우선 탐색이라고 불리며, 상세 동작을 봤을 때 상단 > 자식 노드 > 자식노드의 자식노드 이런식으로 탐색하는 방식이다.
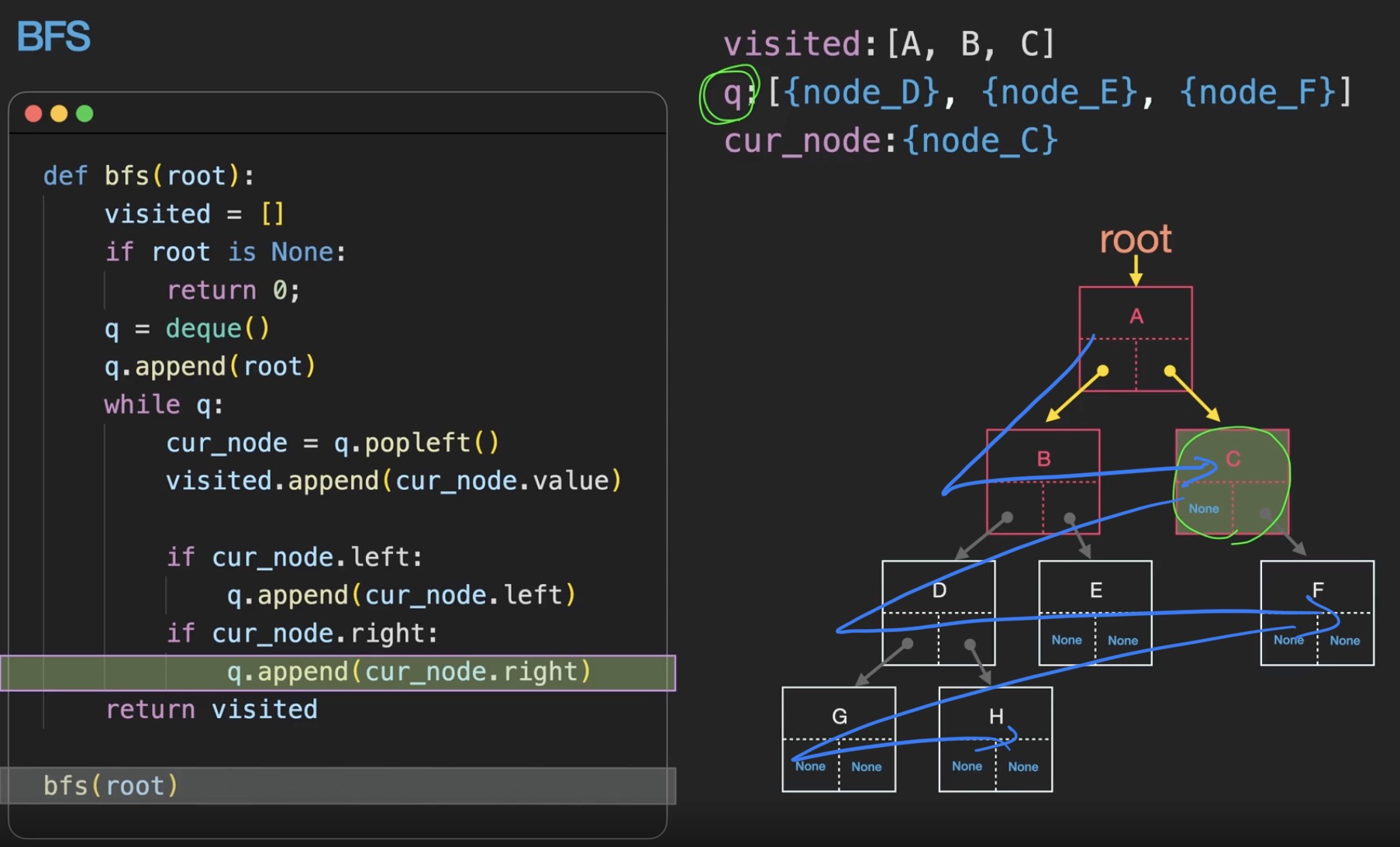
def bfs(root: Node) -> list :
visited = []
if root is None :
return []
q = deque()
q.append(root)
while q :
cur_node = q.popleft()
visited.append(cur_node.value)
if cur_node.left :
q.append(cur_node.left)
if cur_node.right :
q.append(cur_node.right)
return visited
print(bfs(bt.root))DFS (Depth-First Search)
깊이 우선 탐색, 특정 방향의 가장 깊은 곳 > 얕은 곳으로 짚고 넘오는 형식의 탐색 방법

def dfs(root: Node) :
if root is None :
return
dfs(root.left)
dfs(root.right)전위순회(preorder)
자식 노드에 방문하기 전에 자기 자신부터 방문을 한다.
visited = []
def dfs(node: Node) :
if node is None :
return
visited.append(node)
dfs(node.left)
dfs(node.right)중위순회(inorder)
왼쪽에 있는 모든 노드를 확인하고 나서 자기 자신을 확인하는 방식이다.
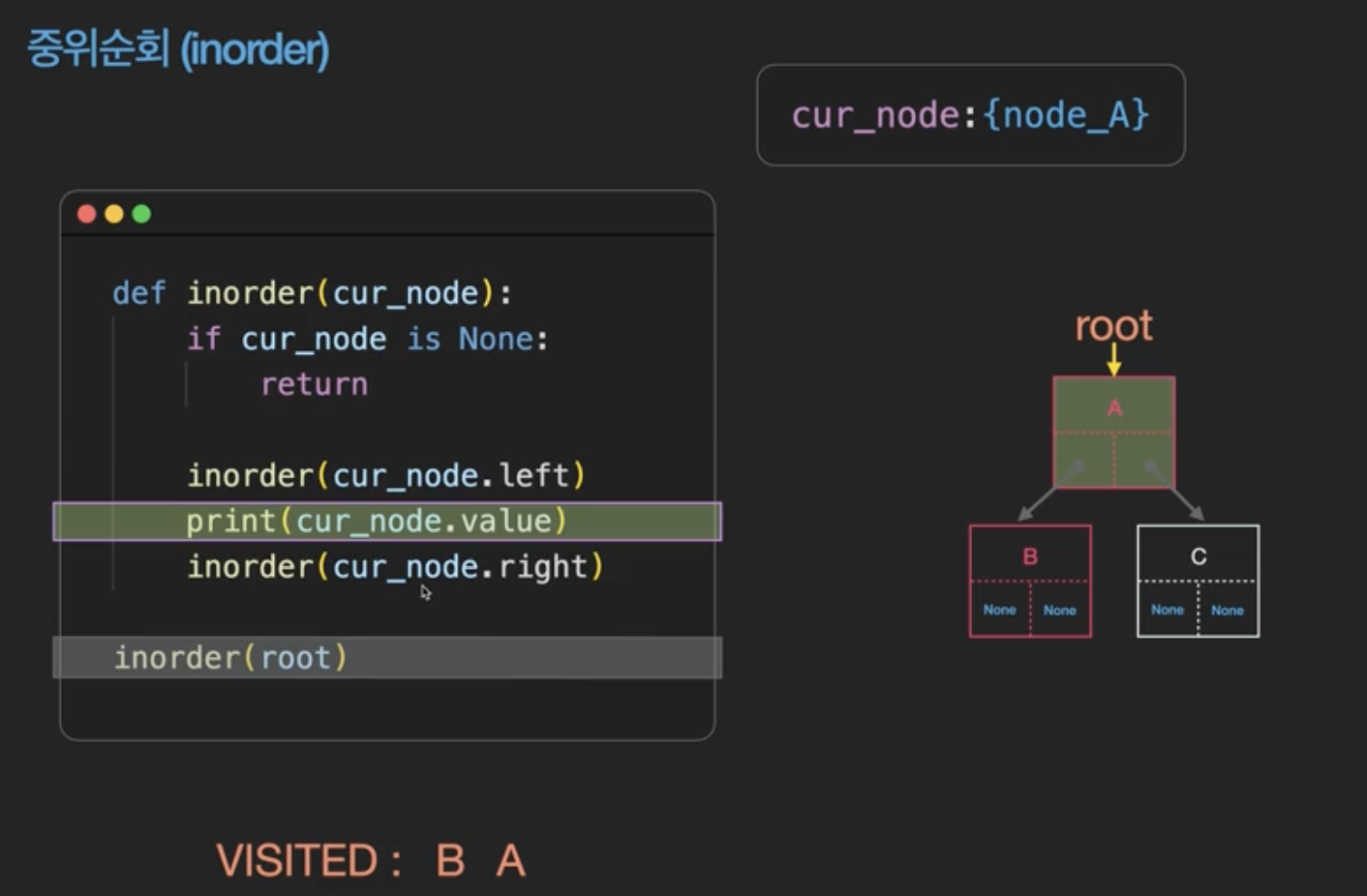
visited = []
def dfs(node: Node) :
if node is None :
return
dfs(node.left)
visited.append(node)
dfs(node.right)후위순회(postorder)
자식을 다 방문한 다음에 자기 자신을 방문하는 방식이다.
visited = []
def dfs(node: Node) :
if node is None :
return
dfs(node.left)
dfs(node.right)
visited.append(node)세그먼트 트리(Segment Tree)
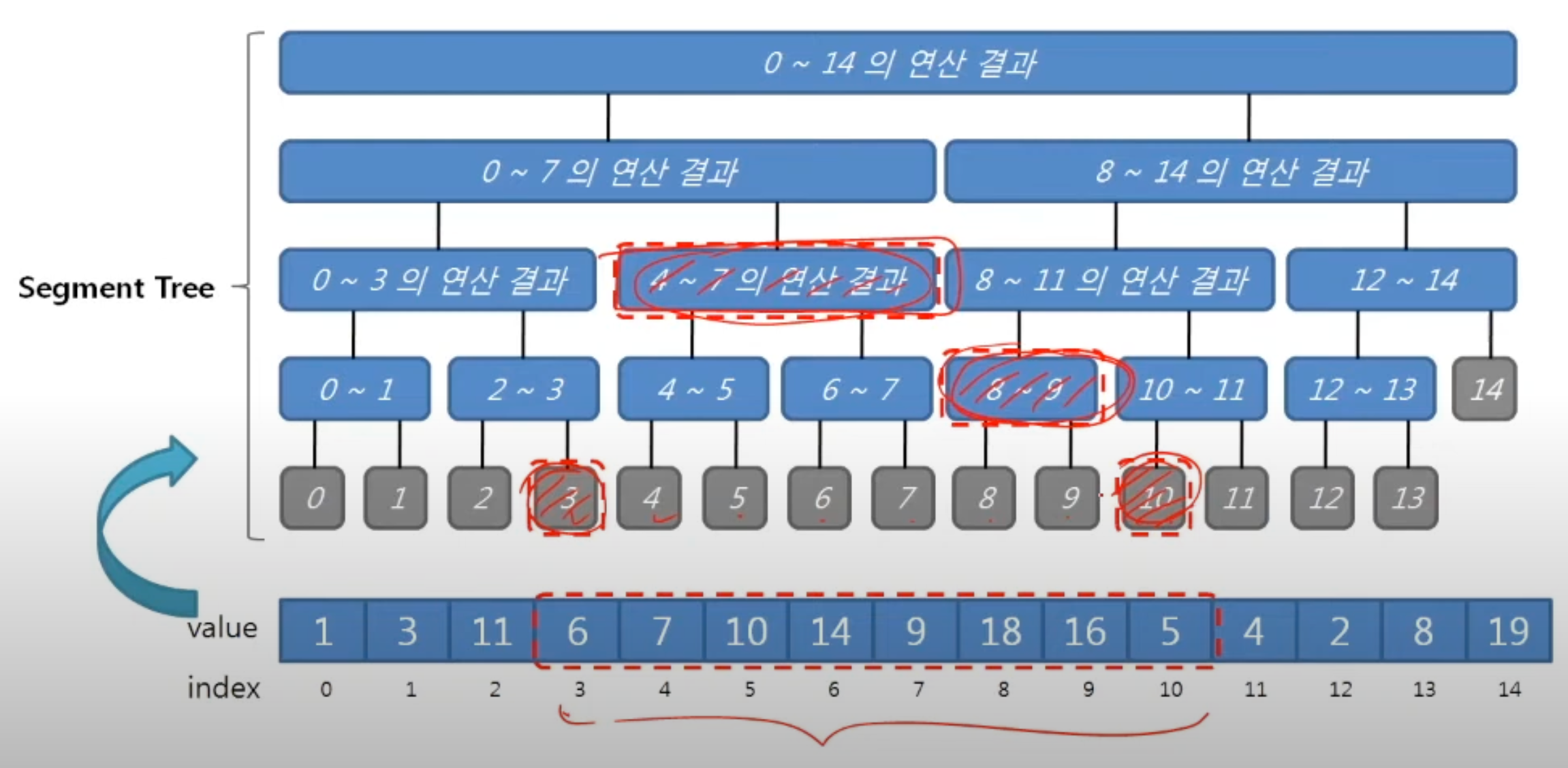
세그먼트 트리는 부모가 왼쪽 자식과 오른쪽 자식의 합을 가지는 구조의 완전 이진 트리(complete tree) 이다.
전체 코드
- index는 1부터 시작된다.
- init, sum, update 세 부분으로 나눠서 생각하면 좋을 것 같다.
class SegmentTree {
long[] tree; // 각 원소가 담길 트리
int treeSize; // 트리 크기
long[] arr; // 누적합을 구할 기존 배열
public SegmentTree(long[] arr) {
this.arr = arr;
// 트리 높이 구하기
int h = (int) Math.ceil(Math.log(arr.length) / Math.log(2));
this.treeSize = (int) Math.pow(2, h + 1);
// 배열 생성
tree = new long[treeSize];
}
// arr = 원소배열, node = 현재노드, start = 현재구간 배열 시작, end = 현재구간 배열 끝
public long init(int node, int start, int end) {
// 배열의 시작과 끝이 같다면 leaf 노드이므로
// 원소 배열 값 그대로 담기
if (start == end) {
return tree[node] = arr[start];
}
// leaf 노드가 아니면, 자식노드 합 담기
return tree[node] =
init(node * 2, start, (start + end) / 2)
+ init(node * 2 + 1, (start + end) / 2 + 1, end);
}
// node: 현재노드 idx, start: 배열의 시작, end:배열의 끝
// idx: 변경된 데이터의 idx, diff: 원래 데이터 값과 변경 데이터값의 차이
public void update(int node, int start, int end, int idx, long diff) {
// 만약 변경할 index 값이 범위 바깥이면 확인 불필요
if (idx < start || end < idx) return;
// 차를 저장
tree[node] += diff;
// 리프노드가 아니면 아래 자식들도 확인
if (start != end) {
update(node * 2, start, (start + end) / 2, idx, diff);
update(node * 2 + 1, (start + end) / 2 + 1, end, idx, diff);
}
}
// node: 현재 노드, start : 배열의 시작, end : 배열의 끝
// left: 원하는 누적합의 시작, right: 원하는 누적합의 끝
public long sum(int node, int start, int end, int left, int right) {
// 범위를 벗어나게 되는 경우 더할 필요 없음
if (left > end || right < start) {
return 0;
}
// 범위 내 완전히 포함 시에는 더 내려가지 않고 바로 리턴
if (left <= start && end <= right) {
return tree[node];
}
// 그 외의 경우 좌 / 우측으로 지속 탐색 수행
return sum(node * 2, start, (start + end) / 2, left, right) +
sum(node * 2 + 1, (start + end) / 2 + 1, end, left, right);
}
}사용예시
// 수 저장 배열
long[] arr = new long[n+1];
for(int i = 1; i <= n; i++){
arr[i] = Long.parseLong(br.readLine());
}
SegmentTree stree = new SegmentTree(n);
stree.init(arr,1,1,n);
for(int i = 0; i < m+k; i++){
st = new StringTokenizer(br.readLine());
// 명령어
int cmd = Integer.parseInt(st.nextToken());
int a = Integer.parseInt(st.nextToken());
// 원소의 범위는 2^63이므로 롱타입으로 받아야한다.
long b = Long.parseLong(st.nextToken());
// 데이터 변경 명령어
if(cmd == 1){
stree.update(1,1,n,a,b-arr[a]);
arr[a] = b;
// 구간합 명령어
}else{
bw.write(stree.sum(1,1,n,a,(int)b) +"\n");
}
}