큐와 스택
이 저작물은 개발남노씨 - 코딩테스트 [ ALL IN ONE ] (opens in a new tab)을 참고하여 작성되었습니다.
Reference
본 게시물은 개발남노씨 - 코딩테스트 ALL IN ONE (opens in a new tab) 강좌를 참고하였습니다.
Queue
시간 순서상 먼저 저장한 데이터가 먼저 출력되는 선입선출형 자료형.
Queue의 뒤쪽에 데이터를 추가하는 것을 enqueue라고 하고, 앞쪽에서 데이터를 꺼내는 것을 dequeue라고 한다.
파이썬에서는 Queue를 deque이라고 부른다.
- deque : Ooubly Ended Queue의 줄임말로, 앞과 뒤에서 즉, 양방향에서 데이터를 처리할 수 있는 Queue형 자료구조이다.
리스트로 Queue를 구현하기
리스트에서 Queue를 구현햇을 경우 pop을 해준 이후 n-1개의 List를 앞으로 한 칸씩 옮기는 작업이 필요하다. 이로 인해서 `pop을 할 때 마다 시간 복잡도 big O(n)번의 시간이 소요된다.
q = []
q.append(1)
q.append(2)
...
for _ in range(100) :
q.pop(0)deque
from collections import deque
# 선언
q = deque()
# 추가
q.appendleft(10)
q.appendleft(11)
q.appendleft(12)
q.append(9) # 12, 11, 10, 9 출력
print(q)
# 삭제
q.popleft()
q.pop()
print(q) # 11, 10 출력rotate
양수는 시계 방향 회전, 음수는 반시계 방향 회전을 하고 2를 넣으면 2칸만큼 회전 4를 넣으면 4칸만큼 회전한다.
시간 복잡도는 O(n)이며, n은 회전할 개수를 의미하며, 반환값은 없다.
this 연산을 사용해서 rotate를 하는 것 같다.
q = deque([1,2,3,4,5])
q.rotate(2)
print(q) # deque([4, 5, 1, 2, 3]Priority Queue
우선순위 큐는 데이터마다 우선순위를 부여하여 우선순위가 높은 데이터가 먼저 출력되는 자료형이다.
완전이진트리로 Priority Queue를 구현할 때 시간복잡도가 O(logN)으로 가장 적다.
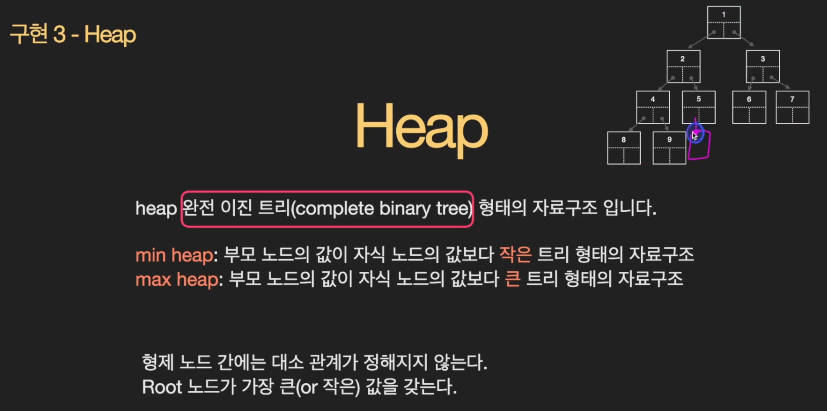
Heap
- min heap : 부모 노드의 값이 자식 노드의 값보다 작은 트리 형태의 자료구조
- max heap : 부모 노드의 값이 자식 노드의 값보다 큰 트리 형태의 자료구조
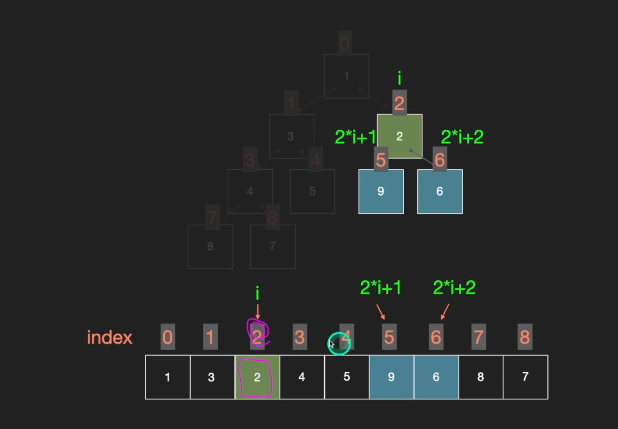
list로 트리를 구성하는 방법
완전 이진 트리에서는 i번째 노드의 부모 노드는 (i-1)//2, 왼쪽 자식 노드는 2i, 오른쪽 자식 노드는 2i+1이다.
이와같은 성질을 이용해서 Heap을 구현할 수 있다.
Min Heap
파이썬에서는 heapq 모듈을 통해서 Heap을 구현할 수 있다.
- heapify : 리스트를 힙으로 변환해준다.
- heappush : 힙에 원소를 추가해준다.
- heappop : 힙에서 원소를 삭제해준다.
import heapq
min_heap = [5,3,9,4,1,2,6]
heapq.heapify(min_heap)
heapq.heappush(min_heap, 7)
result = []
while min_heap :
result.append(heapq.heappop(min_heap))
# [1, 2, 3, 4, 5, 6, 7, 9]
print(result)Max Heap
max heap을 구현할 때는 list의 모든 값들에 -1을 곱해서 min_heap을 하게 되면 max_heap을 구현할 수 있다. 이 때, 결과로 도출해낸 값들에 다시 -1을 곱해줘야 한다.
import heapq
min_heap = [5,3,9,4,1,2,6]
min_heap = [i*-1 for i in min_heap]
heapq.heapify(min_heap)
heapq.heappush(min_heap, 7 * -1)
result = []
while min_heap :
result.append(heapq._heappop_max(min_heap) * -1)
# [9, 6, 2, 3, 1, 4, 5, 7]
print(result)Stack
먼저 저장한 데이터가 나중에 출력되는 후입선출형 자료형.
stack = []
stack.append(1)
stack.appned(2)
stack.appned(3)
print(stack.pop()) # 3 출력
print(stack.pop()) # 2 출력
print(stack.pop()) # 1 출력문제 1 유효한 괄호
https://leetcode.com/problems/valid-parentheses/ (opens in a new tab)
내 풀이
class Solution:
def isValid(self, s: str) -> bool:
m = {}
s_list = list(s)
m_list = ['(',')', '{', '}', '[', ']']
for n in range(len(m_list)) :
m[m_list[n]] = 0
for _ in range(len(s)) :
m[s_list.pop()] += 1
for n in range(3) :
if m[m_list[n*2]] != m[m_list[n*2 + 1]]:
return False
return True문제점
문제상에서 나오는 input들로는 문제가 발생하지 않지만
s = "{{))}}(("와 같은 input이 들어올 경우 문제가 발생한다. 위의 문자열은 분명 유효한 괄호가 아닌데 숫자 쌍이 맞다는 이유로 True를 반환하기 때문이다.
배운점
- list에 not을 하면 list가 비어있는지 확인할 수 있다.
s = []
print(not s) # False강사님 풀이
기본적으로 스택에 '('이 있다면 ')'을 pop할 수 있지 않을까? 라는 생각에서 접근했다.
class Solution:
def isValid(self, s: str) -> bool :
stack = []
for p in s :
if p == "(" :
stack.append(")")
elif p == "[" :
stack.append("]")
elif p == "{" :
stack.append("}")
# stack이 비어있거나 마지막으로 들어간 값과 현재의 값이 다를 경우 False를 출력
elif not stack or stack.pop() != p :
return False문제 2 Daily Temperatures
- 문제설명
온도 List를 넣으면 그보다 따뜻해지는 날이 오는 일자를 return 해준다.
강사님 풀이
나는 완전 탐색 밖에 생각이 안나서 시간초과가 나서 풀지 못했다.
- 문제 풀이 생각? :
- 스택의 최상단에는 항상 최저온도가 있다.
- 현재 온도가 스택의 최상단 온도보다 클 때 stack에 들어있던 시간을 구해야 한다.
class Solution:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
ans = [0] * len(temperatures)
stack = []
for cd, cv in enumerate(temperatures) :
while stack and stack[-1][1] < cv :
pd, _ = stack.pop()
ans[pd] = cd - pd
stack.append((cd, cv))
return ans